Assalamualaikum w.b.t, saya MOHAMMAD ARIFF FARHAN BIN ZULKARIA (13DEM19F1035) dari kelas DEM2S1 ingin menceritakan tentang PRESSURE AND DEPTH yang dibentangkan oleh ENCIK ROSHAIZUL NIZAM BIN SANI.










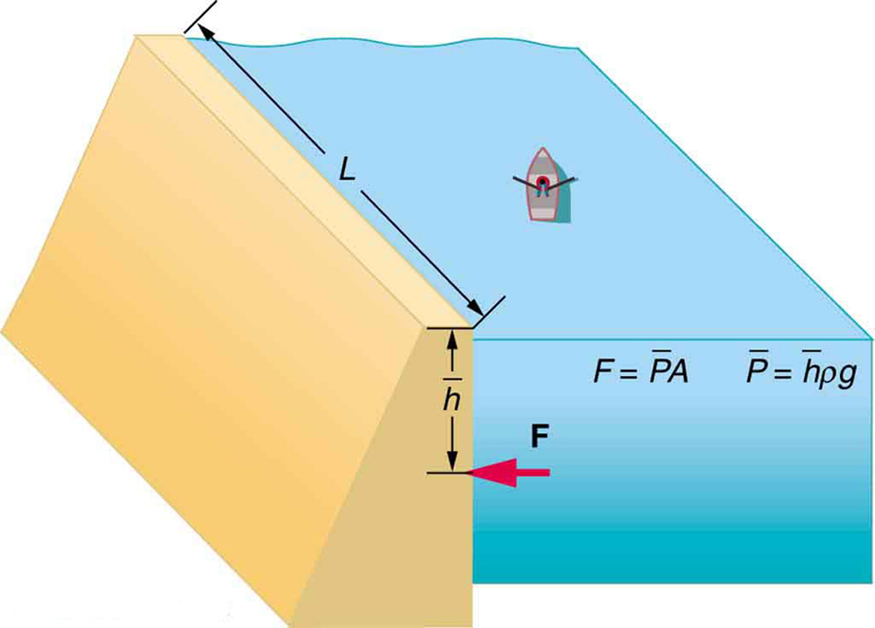
 of the weight. Note that the pressure found in part (a) is completely independent of the width and length of the lake—it depends only on its average depth at the dam. Thus the force depends only on the water’s average depth and the dimensions of the dam, not on the horizontal extent of the reservoir. In the diagram, the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure.epth to balance the increasing force due to the increasing pressure.
of the weight. Note that the pressure found in part (a) is completely independent of the width and length of the lake—it depends only on its average depth at the dam. Thus the force depends only on the water’s average depth and the dimensions of the dam, not on the horizontal extent of the reservoir. In the diagram, the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure.epth to balance the increasing force due to the increasing pressure.
We also can see about pressure and depth in link https://www.youtube.com/watch?v=5EWjlpc0S00 and https://www.youtube.com/watch?v=K5g6P8-GmBg
That's all from me to present about pressure and depth.
If your ears have ever popped on a plane flight or ached during a deep dive in a swimming pool, you have experienced the effect of depth on pressure in a fluid. At the Earth’s surface, the air pressure exerted on you is a result of the weight of air above you. This pressure is reduced as you climb up in altitude and the weight of air above you decreases. Under water, the pressure exerted on you increases with increasing depth. In this case, the pressure being exerted upon you is a result of both the weight of water above you and that of the atmosphere above you. You may notice an air pressure change on an elevator ride that transports you many stories, but you need only dive a meter or so below the surface of a pool to feel a pressure increase. The difference is that water is much denser than air, about 775 times as dense.
Consider the container. Its bottom supports the weight of the fluid in it. Let us calculate the pressure exerted on the bottom by the weight of the fluid. That pressure is the weight of the fluid  divided by the area
divided by the area  supporting it (the area of the bottom of the container):
supporting it (the area of the bottom of the container):
We can find the mass of the fluid from its volume and density:
The volume of the fluid  is related to the dimensions of the container. It is
is related to the dimensions of the container. It is
where  is the cross-sectional area and
is the cross-sectional area and  is the depth. Combining the last two equations gives
is the depth. Combining the last two equations gives
If we enter this into the expression for pressure, we obtain
The area cancels, and rearranging the variables yields
This value is the pressure due to the weight of a fluid. The equation has general validity beyond the special conditions under which it is derived here. Even if the container were not there, the surrounding fluid would still exert this pressure, keeping the fluid static. Thus the equation  represents the pressure due to the weight of any fluid of average density
represents the pressure due to the weight of any fluid of average density  at any depth
at any depth  below its surface. For liquids, which are nearly incompressible, this equation holds to great depths. For gases, which are quite compressible, one can apply this equation as long as the density changes are small over the depth considered.Illustrates this situation.
below its surface. For liquids, which are nearly incompressible, this equation holds to great depths. For gases, which are quite compressible, one can apply this equation as long as the density changes are small over the depth considered.Illustrates this situation.
The bottom of this container supports the entire weight of the fluid in it. The vertical sides cannot exert an upward force on the fluid (since it cannot withstand a shearing force), and so the bottom must support it all.
Calculating the Average Pressure and Force Exerted: What Force Must a Dam Withstand?
We calculated the mass of water in a large reservoir. We will now consider the pressure and force acting on the dam retaining water. The dam is 500 m wide, and the water is 80.0 m deep at the dam. (a) What is the average pressure on the dam due to the water? (b) Calculate the force exerted against the dam and compare it with the weight of water in the dam (previously found to be  ).
).
Strategy for (a)
The average pressure 
due to the weight of the water is the pressure at the average depth
of 40.0 m, since pressure increases linearly with depth.
due to the weight of the water is the pressure at the average depth
of 40.0 m, since pressure increases linearly with depth.
Solution for (a)
The average pressure due to the weight of a fluid is
Entering the density of water from and taking  to be the average depth of 40.0 m, we obtain
to be the average depth of 40.0 m, we obtain
Strategy for (b)
The force exerted on the dam by the water is the average pressure times the area of contact:
Solution for (b)
We have already found the value for  . The area of the dam is
. The area of the dam is  , so that
, so that
Discussion
Although this force seems large, it is small compared with the  weight of the water in the reservoir—in fact, it is only
weight of the water in the reservoir—in fact, it is only
The dam must withstand the force exerted against it by the water it retains. This force is small compared with the weight of the water behind the dam.

We also can see about pressure and depth in link https://www.youtube.com/watch?v=5EWjlpc0S00 and https://www.youtube.com/watch?v=K5g6P8-GmBg
That's all from me to present about pressure and depth.

Ulasan
Catat Ulasan